
This article presents the logistic map as a simple model suitable for introducing students to the properties of dynamical systems including periodic orbits, bifurcations, and deterministic chaos. The population level at any given time is a function of a growth rate parameter and the previous time step’s population level. 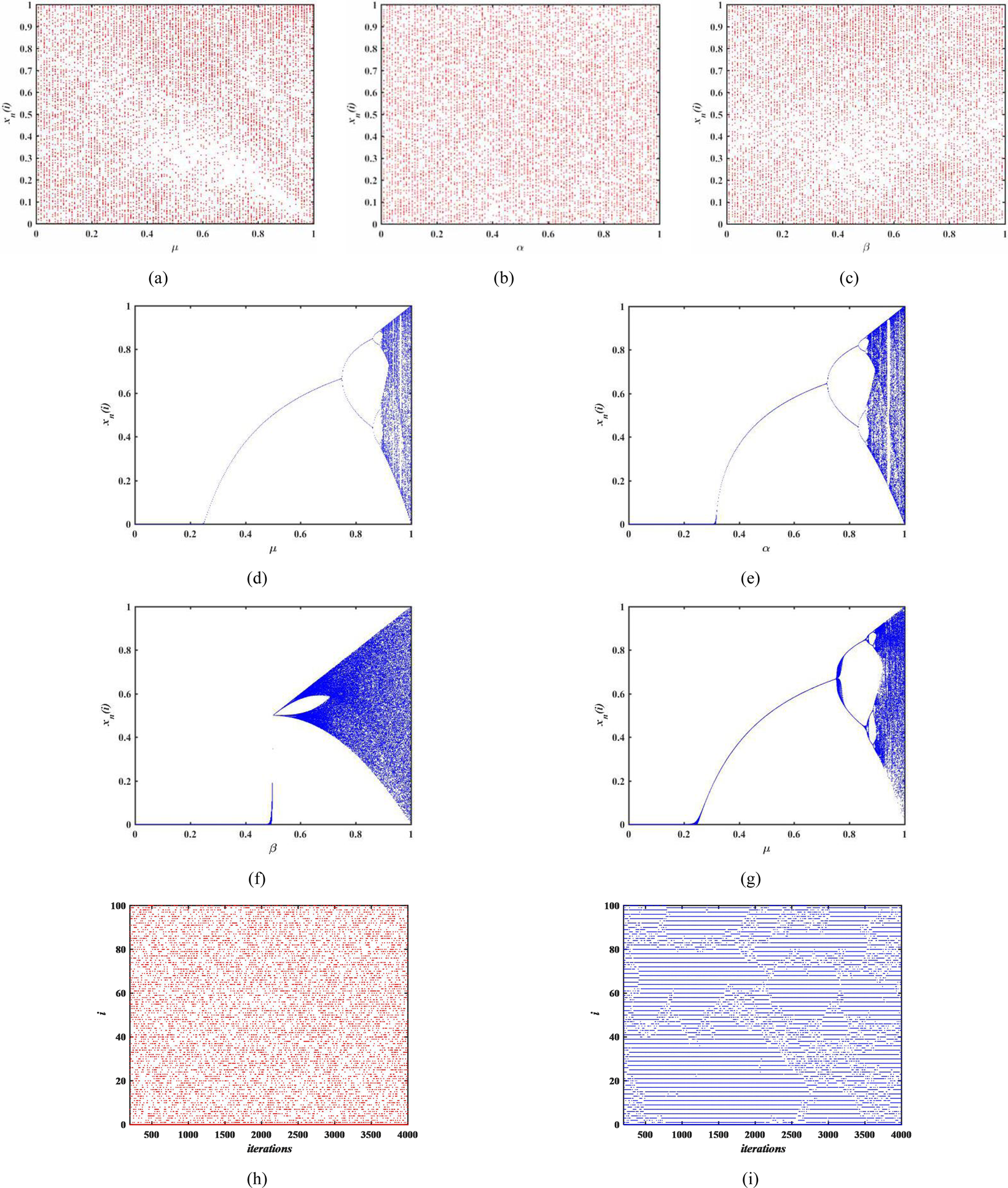

The logistic map is a simple function that models growth dynamics by mapping a population’s value at any time step to its value at the next time step.
Background: Chaos and the Logistic Model. The logistic map is defined by the following equation: x n + 1 = λ x n. Historically it has been one of the most important and paradigmatic systems during the early days of research on deterministic chaos. The logistic map is a one-dimensional discrete-time map that, despite its formal simplicity, exhibits an unexpected degree of complexity. 
Traditionally, this discrete chaos is controlled by one parameter $$\\lambda $$ λ using Picard orbit, a one-step.
With a vital role of discrete chaos, standard logistic map has found a celebrated place in the dynamics of chaos theory and in various applications of science, such as a discrete traffic flow model, image encryption in cryptography, secure communication, and weather forecasting. chaos-theory numerical-analysis logistic-map secant-method. I increase the number of digits in the accumulation point computation using sequence acceleration techniques. I calculate the sequence of superstable points R_n using non-derivative root-finding methods. Computation of the logistic map's period-2 accumulation point. 
Using Magnify, determine the approximate s-value at which the 3-cycle window opens (the first appearance of the 3-cycle) and the value at which the 3-cycle window closes (where full-blown chaos returns). Exercises for Chaos Under Control Chapter 5: Surprises in the Dynamics of the Logistic Map.








 0 kommentar(er)
0 kommentar(er)
